Du kannst die antiproportionale Zuordnung immer mit dem umgekehrten (antiproportionalen) Dreisatz lösen. Der antiproportionalen Dreisatz überzeugt durch seine Übersichtlichkeit: aus genau drei gegebenen Zahlenwerten kann der vierte gesuchte ermittelt werden – oder es kann der vierte gegebene dahingehend überprüft werden, ob er einer antiproportionalen Zuordnung entspricht!
Mit dem online Dreisatzrechner kannst du schnell überprüfen, ob es sich um proportionale oder antiproportionale Zuordnungen handelt. In diesem Beitrag findest du ausgewählte Aufgaben, Tipps und Tricks sowie einen kompletten offline Dreisatzrechner zum Downloaden.
Downloads
Die folgenden Downloads enthalten die vorliegende Seite als PDF-Datei, antiproportionale Beispiele mit Lösungen und eine Microsoft Excel Version von Dreisatzrechner. Du solltest aber noch die unten stehende Informationen zu diesem Kapitel kurz noch sehen, um die Downloads schnell und richtig verwenden zu können.
- Antiproportionale Aufgaben und Lösungen
- Diese Beitragsseite zum Ausdrucken als PDF-Datei
- Microsoft Excel Version: der offline Dreisatzrechner
![]()
Antiproportionale Zuordnung – theoretischer Hintergrund
Jede Textaufgabe zum Thema „antiproportionale Zuordnung“ beschreibt immer eine Situation, in der von einer Sache weniger wird, wenn von einer anderen Sache mehr wird. Wenn sich diese Änderungen zusätzlich umgekehrt proportional zueinander verhalten, dann ist es eindeutig eine antiproportionale Zuordnung.
Eine solche Textaufgabe ist meistens durch folgende vier Checkpunkte definiert:
- Meistens sind genau 3 Zahlenwerte gegeben. Falls mehr Zahlenwerte gegeben sind, dann handelt es sich entweder um reine Zusatzinformationen oder es handelt sich um den zusammengesetzten Dreisatz, siehe Beispiel unten)
- 2 Zahlenwerte davon haben die gleiche Einheit (zum Beispiel: Kilometer, Stück, Liter,…)
- Der dritte Zahlenwert hat meist eine andere Einheit (zum Beispiel: Sekunden, Geschwindigkeit,…)
- Es gilt die Regel: je mehr, desto weniger bzw. je weniger, desto mehr.

Zusätzlich muss die umgekehrte Proportionalität gelten, d.h. wenn ich doppelt so viel von der einen Sache habe, dann soll halb so viel von der anderen Sache herauskommen.

Tipp:
Ein besonders häufiges Thema ist die Baustelle. Hier tauchen Fragen auf wie:
- wie viel Baumaschinen muss ich zusätzlich einsetzen, um weniger Zeit zu verbrauchen
- wie viel Arbeiter muss sich einstellen, um entsprechend schneller eine Arbeit zu verrichten

Ein anderes sehr häufiges Thema ist der Straßenverkehr und die Geschwindigkeit:
- je schneller ich fahre, umso weniger Zeit verbrauche ich
Ein paar kleine Gegenbeispiele dazu:
Ein Alublech ist 2 mm dick, hat eine Fläche von 2 m² und liegt 1,2 kg. Wie viel wiegt ein 3 mm dickes Alublech mit einer Fläche von 2,4 m²?
In diesem Fall gibt es folgende Zahlenwerte: 2 mm, 2 m², 1,2 kg, 3 mm, 2,4 m². Es sind also fünf Zahlenwerte gegeben und es kommen drei verschiedene Einheiten (Millimeter, Quadratmeter, Kilogramm) vor. Damit handelt es sich ganz eindeutig nicht um eine proportionale Zuordnung im eigentlichen Sinn, sondern um den zusammengesetzten Dreisatz – diese wird in einem separaten Beitrag ausführlich behandelt, siehe dort.
Otto kann in 3 Minuten 5 Äpfel essen. Wie lange braucht er, um 7 Äpfel zu essen?
Hier kommen folgende Zahlenwerte vor: 3 Minuten, 5 Äpfel, 7 Äpfel. Damit ist erst die Bedingungen gegeben. Auch kommen zwei unterschiedliche Einheiten vor: Minuten und Äpfeln. Damit ist die zweite Bedingung erfüllt. Allerdings gilt, je mehr Äpfel gegessen werden umso mehr Minuten werden vergehen. Also je mehr, desto mehr… Damit handelt es sich nicht um eine antiproportionale, sondern um eine proportionale Problemstellung.
Zwei Traktoren kann eine gewisse Größe von Ackerland in 30 Stunden pflügen. Vier Traktoren brauchen 16 Stunden, acht Traktoren brauchen 9 Stunden, wie lange brauchen 16 Traktoren?
Es gibt folgende Zahlenwerte:2, 4, 8, 16 Traktoren sowie 30,16, 9 Stunden. Da es in diesem Fall mehr als drei Zahlenwerte sind, muss überprüft werden ob es sich tatsächlich um eine „proportionale“ bzw. „antiproportionalen“ Zuordnung handelt. Die Anzahl der Traktoren verdoppelt sich jeweils, die zugehörigen Stunden halbieren sich nicht, damit handelt es sich nicht um eine umgekehrt proportionale Zuordnung. Diese Textaufgabe muss eine andere Art und Weise gelöst werden!
![]()
Und nun ein positives Beispiel:
5 Hühner fressen den Futtertrog in 21 Minuten leer. Wie lange brauchen 7 Hühner dazu?
Es kommen folgende Zahlenwerte vor: 5 Hühner, 21 Minuten, 7 Hühner. Damit ist erst Bedingung erfüllt. Es kommen folgende Einheiten vor: Hühner und Minuten. Damit ist die zweite und dritte Bedingung erfüllt. Es gilt die Regel: je mehr Hühner desto weniger Minuten. Damit ist die vierte Bedingung erfüllt: in diesem Fall handelt es sich um eine klassische Problemstellung für den umgekehrt antiproportionalen Dreisatz bzw. die antiproportionalen Zuordnung.
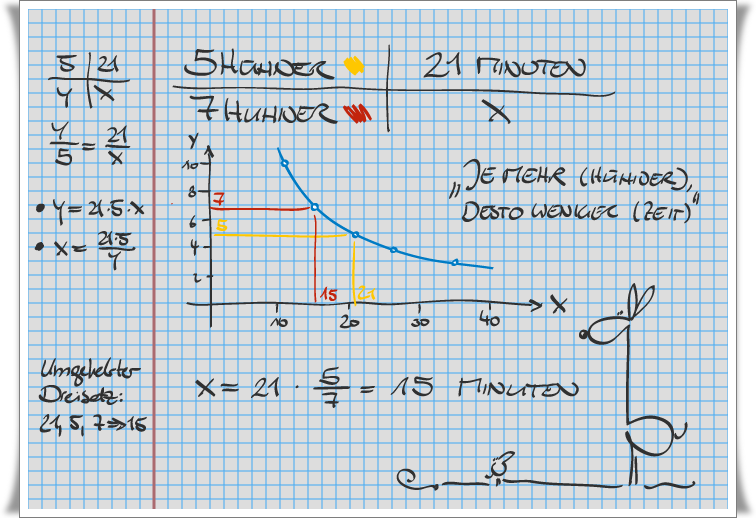

Antiproportionale Zuordnung Aufgaben
Es gibt 13 Gewinner bei einer Lotterie. Jeder erhält 783 Euro. Drei von ihnen verzichten auf ihren Gewinn. Wie viel erhalten die restlichen 10, wenn der Gesamtbetrag vollständig ausgeschüttet werden muss?
X = 783 x 13 / 10 = 1017,90 Euro
Die Benzinreserven auf einer Sibirien-Expedition mit 3 Lastkraftwagen reichen noch für 7.300 km. Wie groß ist die Reichweite, falls ein Lastkraftwagen stehen gelassen wird und die Expedition nur noch mit zwei Wagen fortgesetzt werden soll?
X = 7.300 x 3 / 2 = 10.950 Kilometer
4 Bagger benötigen 12 Tage, um die Baugrube auszuheben. Wie viel Bagger müssen eingesetzt werden, um die Baugrube in 8 Tagen fertig zu stellen?
X = 4 x 12 / 8 = 6 Bagger
Ein Malereibetrieb übernimmt einen Auftrag zum ausmalen eines Einkaufscenters. Das Einkaufscenter muss in zwei Tagen fertig gestrichen sein. Der Malermeister weiß, dass er gemeinsam mit seinen 7 Angestellten dafür 3 Tage braucht. Wie viele zusätzliche Maler muss er beschäftigen, um den Auftrag in zwei Tagen zu schaffen?
X = ( 1 + 7 ) x 2 / 3 = 12
12 – ( 1 + 7 ) = 3 zusätzliche Angestellte
–
Anmerkung zu ( 1 + 7 ): der Malermeister selbst = 1; seine Angestellten = 7
Karl fährt zur Schule mit seinem Fahrrad mit einer Durchschnittsgeschwindigkeit von 12 km/h in 35 Minuten. Wie schnell muss erfahren und bereits in 25 Minuten in der Schule zu sein?
12 x 35 / 25 = 16,8 km/h
![]()
Der Dreisatzrechner in Aktion
Im Downloadbereich kannst du diesen Downloadrechner herunterladen. Er präsentiert dir den kompletten Lösungsweg für jede umgekehrte Dreisatz Aufgabe bzw. antiproportionale Zuordnung. Er ist eine ganz normale Microsoft Excel Datei, ist kostenlos und du kannst selber damit herumexperimentieren. Er kann zusätzlich auch proportionale Probleme lösen.
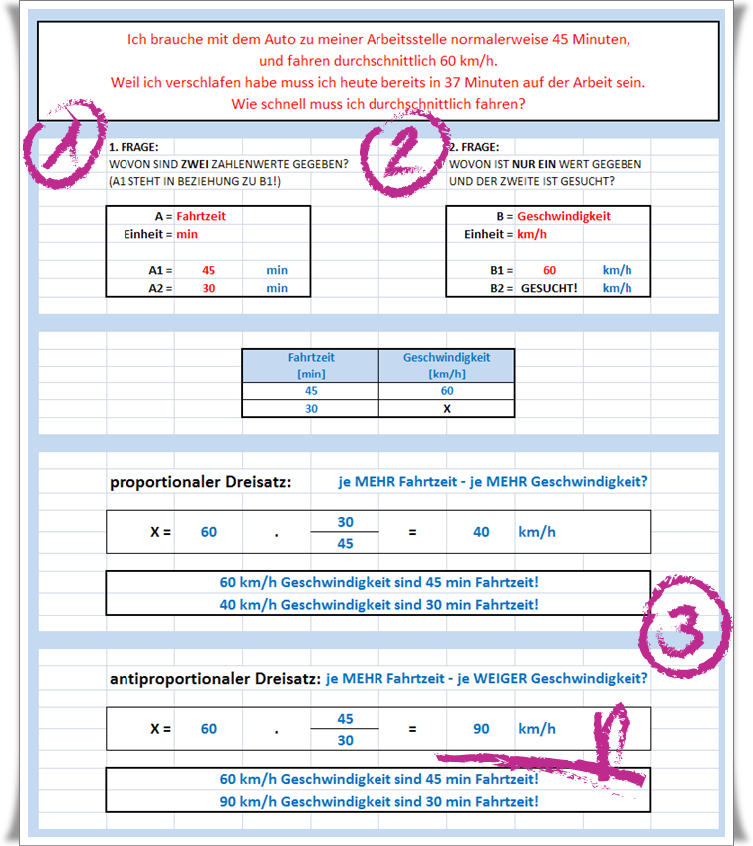
Bitte beachte, dass du nur die roten Texte änderst. Alle blauen Texte enthalten Formeln, wenn du sie überschreibst, funktioniert der Rechner natürlich nicht mehr. Alle schwarzen Zahlen enthalten nur Informationen, ein Überschreiben dieser Werte macht überhaupt keinen Sinn.
So gehst du vor:
- beantworte die Frage: von welcher Einheit sind zwei Zahlenwerte gegeben-und fülle diese beiden Zahlenwerte in den Kasten A.
- Beantworte die Frage: von welcher Einheit ist nur ein Wert gegeben und der zweite gesucht-und fülle den entsprechenden Wert in den Kasten B.
- Mache jetzt den Test, ob es sich um eine proportionale oder antiproportionalen Zuordnung handelt, beantworte also die Frage: gilt – je mehr, desto mehr oder gilt – je mehr, desto weniger?
- Sollten einmal mehr als 3 Werte gegeben sein, zum Beispiel 5 oder 7 oder… dann kannst du überprüfen, ob es sich tatsächlich um eine antiproportionale Zuordnung handelt, indem du jeweils den 4. oder 6. oder 8. oder.. Wert mit dem Rechner ausrechnest und schaust, ob der errechnete Wert mit dem gegebenen Wert übereinstimmt.
Fertig, damit ist jede antiproportionale Zuordnung schnell und einfach gelöst.

