Hier findest du eine bunte Mischung von Dreisatz Aufgaben mit Lösungen. Diese Aufgabensammlung sind farblich nach Schwierigkeitsstufen sortiert. Du erhältst Übungen zum einfachen, umgekehrten und verallgemeinerten Dreisatz sowie zum Zweisatz. Mit dabei ist auch die Prozentrechnung, Strahlensatzaufgaben, Mischrechnungen und vieles mehr. Natürlich kannst du alle Aufgaben auch als PDF-Datei herunterladen – viel Spaß beim Üben und Rechnen.
Downloads
Die folgenden PDF-Dateien sind kostenlos und enthalten Beispielberechnungen, Erklärungen und Lösungen. Sie sind enthalten alle Schwierigkeitsstufe, zusätzlich findest du auch ein kleines Theoriepaket, damit du auch verstehst, was du tust.
Dreisatz Aufgaben
Die nachfolgenden Dreisatzaufgaben sind je nach Schwierigkeitsgrade in folgende Farben eingeteilt:
- gelb = leicht
- orange = schwierig
- rot = für Profis
Tipp: Bei den roten Dreisatz Aufgaben solltest du zusätzlich überprüfen, ob es sich überhaupt um ein Dreisatzproblem handelt. Falls es sich hier um eine Dreisatzübung handelt, kann es auch sein, dass sie nur zu lösen ist, wenn du die 3 Satz Formeln miteinander verschachtelst – probier es einfach aus, du wirst sehen wovon ich rede 😉 hier sind auch ähnliche, nicht direkt mit der Dreisatz Formel in Verbindung stehende Textaufgaben angeführt. Siehe hierzu insbesondere auch die Beiträge zum Mischkreuz, der Prozentrechnung und dem Strahlensatz.
Zu jeder Textaufgabe gibt es eine eindeutige Lösung, in den meisten Fällen ist der wesentliche Lösungsweg skizziert – viel Spaß beim Lernen.
Aufgabensammlung
- Ein Büro als wird von einem Putztrupp mit 24 Putzfrauen in 6 Stunden gereinigt. Wie lange beträgt die Reinigungszeit wenn 2 Putzfrauen krank und 4 Putzfrauen auf Urlaub sind?
Lösung6 / ( 24 – 2 – 4 ) x 24 = 8 Stunden
- Ein Wanderer braucht für 300 Höhenmeter 50 Minuten. Wie lange braucht er, um den Gipfel in 2450 m Seehöhe zu erreichen, wenn er bei einer Höhe von 1250 m Seehöhe startet. Nach jeder vollen Stunde muss er allerdings eine Rast von 12 Minuten einplanen.
Lösung50 / 300 x (2450 – 1250) = 200 min = 3 h + 20 min
3 h + 20 min + 3 x 12 min = 3 h 56 min
_
Dreisatz: Zeit ohne Rast … 50 / 300 x (2450 – 1250)
Ermittlung Anzahl der Rasten: 200 / 60 = 3 h + 20 Rest = 3 Stk - 8 kg lose Äpfel kosten 15,20 €. Wie viel Kilogramm Äpfel bekommst du für 20 €, wenn du ab einem Einkauf von 10 kg 15 % Rabatt erhältst?
Lösung8 / 15,20 x 20 / 0,85 = 12,30 kg
_
Dreisatz … X = 8 / 15,20 x 20
kombiniert mit Prozentrechnung … 15 % Rabatt = Restpreis von 100 – 15 = 85 %
85 % = 85 pro Cent = 85 pro 100 = 85 / 100 = 0,85 - Ein Tank ist zu einem Fünftel mit Wasser gefüllt. Wie viel Liter Wasser sind im Tank, wenn der ¾ volle Tank 120 l Wasser enthält?
Lösung120 / ( 3 / 4) x ( 1 / 5 ) = 32 Liter
- 800 g Schweinefleisch kosten 13,40 €. 700 g Rindfleisch kosten 14,00 €. Wie viel Gramm Rindfleisch kannst du einkaufen, wenn du 40 Euro mit hast und genau 1200 g Schweinefleisch einkaufen musst?Lösung
700 / 14,00 x ( 40 – ( 13,40 / 800 x 1200 ) ) = 995 g
_
Dreisatz: Schwein … 13,40 / 800 x 1200 = 20,10 Euro
Restgeld: 40 – 20,10 = 19,90 Euro
Dreisatz: Rind … 700 / 14,00 x 19,90 = 995 GRAMM - Mein PKW verbraucht bei einer Fahrt nach München 94,9 l Benzin. Wie weit wohne ich von München entfernt, wenn mein Auto einen mittleren Kraftstoffverbrauch von 7,3 l Benzin bei 100 km hat?
Lösung100 / 7,3 x 94,9 = 1300 km
- 3 Hamster fressen 23 Erbsen in 4 Stunden. Wie lange brauchen 5 Hamster für 69 Erbsen?
Lösung( 4 x 60 x 60 ) / 23 x 3 / 5 x 69 = 25920 sec = 7 h + 36 min
_
Umrechnung Stunden in Sekunden: 4 x 60 x 60 = 14400 sec
1. Dreisatz: Zeit pro Erbse1 mal Hamster1: X1 = 14400 / 23 x 3
2. Dreisatz: X1 pro Hamster2 mal Erbse2: X2 = X1 / 5 x 69
Umrechnung Sekunden in Stunden: 25960 / 60 / 60 = 7 + 760 Rest; 760 / 60 = 36 + 0 Rest - Messing ist eine Legierung aus Kupfer und Zink. Du hast eine Messingssorte von 300 kg mit 40 % Zinkanteil. Du möchtest 500 kg mit 55 % Zinkanteil haben. Wie hoch ist der Zinkanteil des beizufügenden Messings?Lösung
300 x 0,40 + ( 500 – 300 ) x PZ = 500 x 0,55
PZ = ( 500 x 0,55 – 300 x 0,40 ) / (500 – 300 ) = 0,775 = 77,5 %
_
Anmerkung: Hier handelt es sich um keine Dreisatzaufgabe!
Du rechnest für jede Messingsorte nur das Gewicht vom Zink aus und erstellst die Gleichung:
Zinkgewicht1 + Zinkgewicht2 = Zinkgewicht3 - Eine Wasserpumpe mit 6 kW fördert 920 m³ Wasser 15 m hoch. Welche Wassermenge könnte eine 10,5 kW starke Pumpe 20 m hoch fördern?Lösung
920 / 6 x 15 / 20 x 10,5 = 1207,5 m³
_
1. Dreisatz: Wassermenge pro Leistung1 mal Höhe1: X1 = 920 / 6 x 15
2. Dreisatz: X1 pro Höhe2 mal Leistung2: X2 = X1 / 20 x 10,5 - Mein defekter Laserdrucker könnte in 2 Minute 48 Seiten drucken. Wie lange braucht dein Reserve-Tintenstrahldrucker, der ca. 20 % langsamer ist, um ein Dokument von 520 Seiten zu drucken?Lösung
( 2 x 60 ) / 48 x 513 / 0,80 = 1620 sec = 27 min + 5 sec
_
Umrechnung Minuten in Sekunden: 2 x 60Dreisatz: Laserzeit X = ( 2 x 60 ) / 48 x 513
Prozentrechnung Tintenstrahlerzeit = X / ( (100 – 20) / 100 ) = X / 0,80
Umrechnung Sekunden in Minuten 1620 / 60 = 27 und 5 Rest - Der Winzer Markus möchte in den Großhandel 5000 l Wein mit 12,5 % Alkohol verkaufen. Er hat eine Charge A, welche 11,2 % Alkohol beinhaltet. Zudem hatte eine Charge B, welche 13,1 % Alkohol hat. Wie viel Liter Wein braucht Markus von der Charge 1 unter Charge 2?Lösung
0,6 Teile von Carche A + 1,3 Teile von Carche B bzw.
6 Teile von Carche A + 13 Teile von Carche B bzw.
6 / ( 6 + 13 ) x 5000 = 1.579 Liter von Charche A und
13 / ( 6 + 13 ) x 5000 = 3.421 Liter von Charche B
_
Anmerkung: Die Umrechnung von „Teile“ in „Liter“ ist im Grunde ein einfacher Zweisatz 😉 - Deine neues Traumauto kostet 23.000 Euro. Du musst 70 % gleich zahlen, die restlichen 30 % kannst du zinsfrei in Leasingraten begleichen. Wie viel Geld brauchst in bar, um heute dein Auto zu holen?Lösung
Anzahlung: 23000 / 100 x 70 = 16.100 €
[Einklappen] - Ein Zirben Schnaps hat 42 % Alkohol. In der Flasche sind 700 ml. Wie viel reiner Alkohol ist in dieser Flasche?Lösung
700 x 42 / 100 = 294 ml (reiner, also 100%iger Alkohol)
[Einklappen] - Du möchtest im Restaurant dem Kellner mindestens 8 % Trinkgeld geben, um nicht geizig zu wirken. Die Rechnung für ein Essen beträgt 22,30 €. Wird sich der Kellner denken, du bist geizig wenn du ihm 24 € gibst und sagst: vielen Dank das passt so?Lösung
Mindesttrinkgeld = 22,30 x 8 / 100 = 1,78 €
Tatsächliches Trinkgelt = 24,00 – 22,30 = 1,70 €
–
Der Kellner wird enttäuscht sein, er wird aber trotzdem freundlich bleiben, da er vermuten wird, dass du die Prozentrechnung noch nicht korrekt beherrschst!
Tipps zum Lösen von Textaufgaben
Fast jede Textaufgabe kann mit dem Dreisatz, oder seinen Variationen (proportional, antiproportional, kombiniert, Zweisatz) gelöst werden. Die Betonung liegt hier auf „fast“.
Ein wichtiges ergänzendes Werkzeug ist die Berechnung von Mischungen mit dem sogenannten Mischkreuz. Dieser Typ von Textaufgaben fällt eigentlich nicht unter die Rubrik Dreisatzechnung, ist aber artverwandt und wird der Vollständigkeit halber hier auch behandelt und und kurz erklärt. Er kann immer angewandt werden, wenn es um das Verdünnung berechnen geht (Einstellen vom Alkoholgehalt eines selbst hergestellten Likör aus, verdünnen von Säuren und Basen und natürlich das direkte Zusammenmischen von Bier und Wein 😉 ):
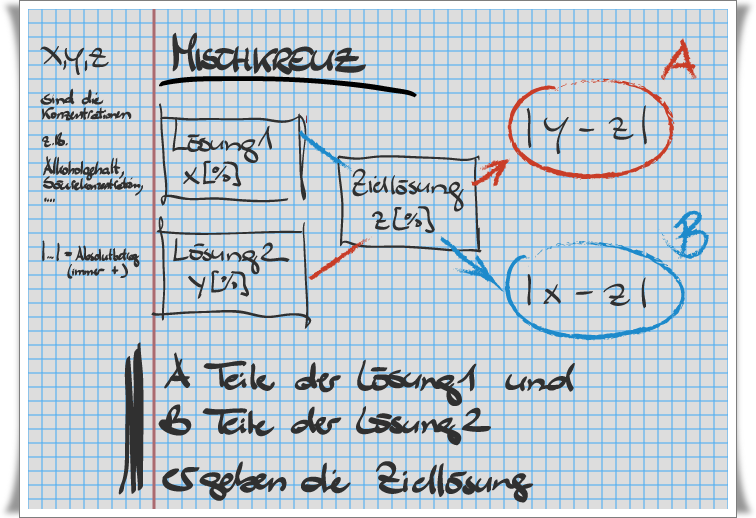
Zusätzlich wird hier auch die Prozentrechnung behandelt. Die Prozentrechnung ist im Grunde nur ein vereinfachter Dreisatz (=Zweisatz), wird in der Literatur aber meist separat behandelt. Die Formel der Prozentrechnung ist am folgenden Beispiel schnell erklärt:
